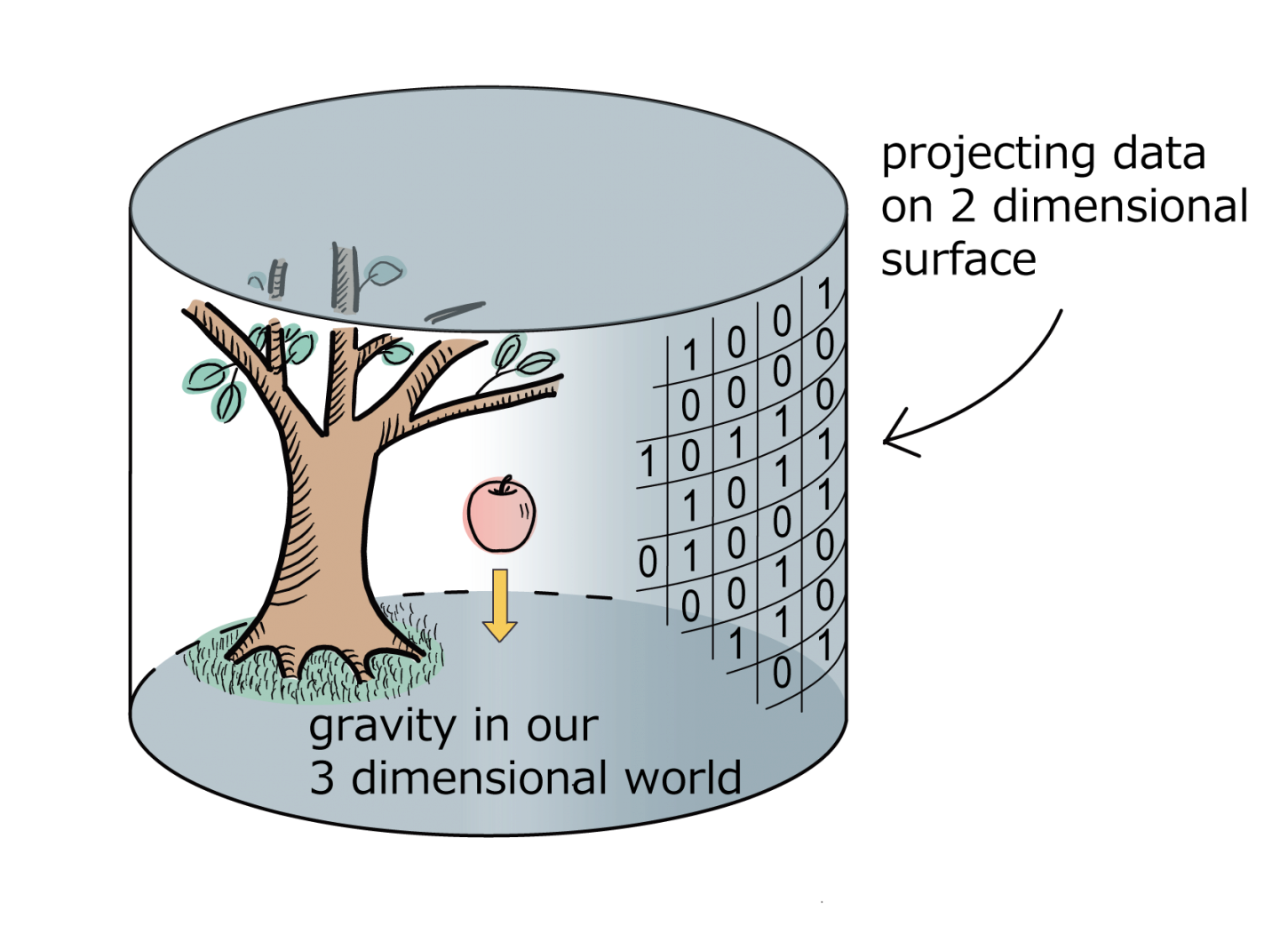
In our group, we employ a quantum information lens to tackle fundamental problems in holography and quantum gravity. One focus is the Ryu–Takayanagi formula and quantum extremal surface (QES)—a powerful tool that relates entanglement entropy in a boundary CFT to the area of extremal surfaces in the bulk geometry. Studying this correspondence illuminates how spacetime regions encode quantum correlations, and offers insights into subregion duality, entanglement wedge reconstruction, and the nature of event horizons. We also investigate multipartite entanglement entropy, extending beyond the simple bipartite case to unveil how multi-party correlations manifest in strongly interacting systems and multi-boundary wormholes. These measures provide a window into richer structures of entanglement that are directly relevant to holographic spacetimes.

​

Beyond entanglement, we explore broader quantum information tools in gravitational contexts. Quantum error correction codes have been proposed as the underlying mechanism of holography, explaining how bulk degrees of freedom become robustly encoded in boundary states. Similarly, the Hayden–Preskill protocol offers a tangible illustration of quantum information scrambling in black hole evaporation, connecting deeply with questions of unitarity and recoverability of quantum states. In parallel, we study quantum chaos—often quantified through out-of-time-ordered correlators or random matrix behavior—to understand how black holes and SYK-like systems saturate known bounds on chaos.